$$\LaTeX$$
Saturday, October 1, 2011
 |
|
1/4
|
2/4
|
3/4
|
|
|
1/8
|
2/8
|
3/8
|
4/8
|
5/8
|
6/8
|
7/8
|
8/8
|
Mica
Introducción
El concepto de probabilidad nace con el deseo del hombre de conocer con certeza los eventos futuros. Es por ello que el estudio de probabilidades surge como una herramienta utilizada por los nobles para ganar en los juegos y pasatiempos de la época. El desarrollo de estas herramientas fue asignado a los matemáticos de la corte. Con el tiempo estas técnicas matemáticas se perfeccionaron y encontraron otros usos muy diferentes para la que fueron creadas. Actualmente se continúo con el estudio de nuevas metodologías que permitan maximizar el uso de la computación en el estudio de las probabilidades disminuyendo, de este modo, los márgenes de error en los cálculos
ACTIVIDAD I
¿Cuál es la probabilidad de que una persona de 25 años de edad llegue hasta los 40 años, si de acuerdo con una tabla de mortalidad cada 93,745 personas de 25 años de edad solo 87,426 llegan a los 40 años? R= 87,426 / 93,745= 0.9325 La probabilidad es de un 93%
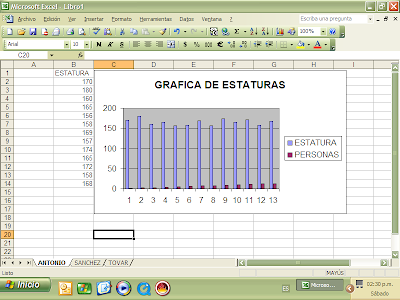
ELABORACIÓN DE UN HISTOGRAMA CONSIDERANDO LAS ESTATURAS DE LOS ALUMNOS DE LA LIC. EN MATEMÁTICA EDUCATIVA.
ESTATURAS ni 156 1 157 1 158 2 160 1 165 2 168 1 169 1 170 1 172 1 174 1 180 1 TOTALES 13
Amplitud del rango
180-156 = 24
13= 3.6 = 4
24/ 4 = 6
Intervalo mi Ni fi Ni Fi
156--162 159 5 5/13=0.384 5 5/13=0.384
162--168 165 2 2/13=0.153 7 7/13=0.538
168--174 171 4 4/13=0.307 11 11/13=0.846
174--180 177 1 1/13=0.076 12 12/13=0.923
180--186 183 1 1/13=0.076 13 13/13=1
Total 13
HISTOGRAMA
ESTATURAS DE ALUMNOS
PROBABILIDAD COMO FRECUENCIA ABSOLUTA
Introducción a la probabilidad.
En la actualidad vemos que la teoría de la probabilidad ocupa un lugar importante en muchos asuntos de negocios. Los seguros y prácticas actuariales se basan firmemente en los principios de la teoría de la probabilidad. Las pólizas de seguros de vida dependen de las tablas de mortalidad, las cuales a su vez se basan en las probabilidades de muerte en edades específicas. Otras tasas de seguros tales como seguro de bienes raíces y de automóviles se determinan de manera similar. La probabilidad también juega un papel importante en la estimación del número de unidades defectuosas en un proceso de fabricación, la probabilidad de recibir pagos sobre cuentas por cobrar y las ventas potenciales de un nuevo producto. Incluso los apostadores profesionales en eventos deportivos deben tener una comprensión sólida de la teoría de la probabilidad.
Problema 1
¿Cuál es la probabilidad de que una persona de 25 años de edad llegue a sobrevivir hasta los 40 si de acuerdo con una tabla de mortalidad, de caa 93 745 personas de 25 años de edad sólo 87 426 llegan a los 40 años.
Solución:
Como h=87426
n=93745
Probabilidad S= personas que llegan a los 40 años = 87 426
Total de personas de 25 años 93 745
= 0.9325 (se tomaron cuatro cifras decimales)
Problema 2
En una caja hay 25 tornillos en buen estado y 80 defectuosos, ¿Cuál es la probabilidad de sacar de la caja un tornillo en buen estado?
Solución:
Como h=25
N=80+25
Probabilidad S= Numero de tornillos en buen estado = 25 = 25
Total de tornillos en la caja 25+80 105
=0.2380
Probabilidad en porcentaje = 0.2380 (100) =23.80%
Problema 3
De cada 1000 personas a las que se les practica una revisión médica, 35 tienen problemas de vista. ¿Cuál es la probabilidad de que una persona examinada tenga alguna enfermedad en los ojos?
Solución:
Como h=35
n= 1000
Probabilidad S = número de personas con problemas de la vista = 35 = 7
Total de personas examinadas 1000 200
Probabilidad en porcentaje = 0.035(100)= 3.5%
Problema 4
En una caja hay 75 canicas azules y 225 rojas, ¿Cuál es la probabilidad de obtener al azar una canica azul?
Solucion:
Como h= 75
n= 75+225
Probabilidad S= numero de canicas azules = 75 = 75
Total de canicas en la caja 75 + 225 300
=0.25
Probabilidad en porcentaje = 0.25 (100)=25%
CONJUNTO POTENCIA
En matemáticas, dado un conjunto S, se llama conjunto potencia o conjunto de partes de S (se denota por P(S) o 2S) al conjunto de todos los subconjuntos de S.
En la teoría de conjuntos basada en los Axiomas de Zermelo-Fraenkel, la existencia del conjunto potencia se establece por el axioma del conjunto potencia. Por ejemplo, si S= {a, b, c} entonces el conjunto potencia de S es P(S) = {{ }, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}.
El conjunto potencia de un conjunto S, junto con las operaciones de la unión, de la intersección y del complemento forman el ejemplo prototípico de álgebra de Boole. De hecho, uno puede demostrar que cualquier álgebra de Boole finita es isomorfa al álgebra booleana del conjunto potencia de un conjunto finito. Para las álgebras booleanas infinitas esto no es verdad, pero cada álgebra booleana infinita es sub-álgebra de una álgebra booleana de parte.
INTRODUCCIÓN
La teoría de conjuntos es una rama de la matemática relativamente moderna cuyo propósito es estudiar unas entidades llamadas conjuntos, aunque otra parte de esta teoría es reconocida como los fundamentos mismos de las matemáticas. La teoría de conjuntos fue desarrollada por el matemático alemán Georg Cantor a finales del siglo XIX a partir de ciertas conclusiones hechas por él mismo al reflexionar en unos detalles de las series trigonométricas de Fourier. La teoría de conjuntos fue expuesta por Cantor en una serie de artículos y libros, de los cuales pueden destacarse sus Beiträge zur Begründung der transfiniten Mengenlehre.
El propósito de Cantor era proporcionar un método para lidiar con asuntos relacionados al infinito actual, un concepto que fue rehuido y rechazado por algunos matemáticos (Pitágoras, Gauss, Kronecker) por considerarlo sin significado.
PROBLEMA
Conjunto potencia de [ 1,2,3, 4]
S= { }, { 1}, {2}, {3}, {4}, {1,2}, {1,3}, {1,4}, {2,3}, {2,4}, {3,4}, {1,2,3}, {1,2,4}, {3,2,4}, {4,3,1}, {1,2,3,4}
PROBABILIDAD DE UNA DIFERENCIA
La probabilidad de una diferencia se aplica cuando se quiere obtener la probabilidad de que un suceso determinado ocurra y que simultáneamente otro suceso, también determinado, no ocurra. Se expresa así:
P(A-B) = P(A) – P(A B)
Problema 25
En una urna hay pelotas rojas numeradas del 1 al 10 y pelotas azules numeradas del 1 al 5. ¿Cuál es la probabilidad de que al extraer al azar una pelota sea roja y no tenga el número 5?
Solución:
A: Se extrae pelota roja
B: Sale el número 5
El suceso que nos interesa es A – B. Aplicamos la relación:
P(A – B) =P(A ) – P(A B) Con
P(A)=10/15
P(A B)=1/15 Porque sólo hay una pelota roja marcada con el número 5 del total de las 15 pelotas. Por lo tanto:
P(A-B)=10/15-1/15=9/15 =0.6000 =60%
Otro procedimiento para resolver este problema es revisando la probabilidad como frecuencia relativa , así: Solución :
Espacio muestral
S=[R1, R2, R3, R4, R5, R6, R7, R8, R9, R10, A1, A2, A3, A4, A5] son sucesos
A: La pelota es roja y no es el número 5
A =[R1, R2, R3, R4, R6, R7, R8, R9, R10) SON 9 (no está R5)
P(A)=casos favorables= 9 = 0.60 =60%es el mismo resultado
-------------------- ---
Casos posibles 15 El resultado que obtuvimos con P(A B)=P(A). P(B)=1/15
También lo podemos obtener con las siguientes relaciones:
P(A - B) = P(A B´) =P(B’ A) Problema 26
La probabilidad de que Antonio gane un juego de tenis es de 2/5 y la probabilidad de que Juan gane es de ¼. ¿cuál es la probabilidad de que Antonio gane el torneo en que participa si en el juego final se enfrenta a Juan?
Solución :
Sucesos
A: Gane Antonio
B: Gane Juan
El suceso que nos interesa es que Antonio gane y simultáneamente que Juan pierda. Por tanto, aplicamos la siguiente relación:
P(A B)= P(A y B) = P(A) . P(B)
=2/5[1/4]=2/20 P(A - B) = P(A) – P(A B)
=2/5-2/20=8-2/20=6/20=0.3 =30% Otro procedimiento para resolver este problema consiste en aplicar la siguiente relación:
P(A –B) = P(A) – P(A B) = P(A B´)
P(A –B) = P(A B’)
Con
P(B’) =1-1/4=4/4-1/4=3/4
Sustituimos en:
P(A – B) =P(A B’)
=P(A) . (B)
=[2/5][3/4]=6/20=0.3 =30 %
PROBLEMA 27
A y B son sucesos donde:
P (A )= P (Aᴒ B´)
P (A ) = 3 4 P (B) = 3 8
P (AᴒB ) = P(BᴒA) = 1 8 Calcular
a) P(A´ᴒB)
b) P(AᴒB´)
c) P(Aᴗ B)
d) P(AᴒB´)
Solucion:
Recordando las relaciones de la probabilidad de una diferencia tenemos:
P(A-B) = P(A) – P (AᴒB)
P(A-B) = P(AᴒB´) – P(B´ᴒA)
a) De 2 intercambiamos A y B
P(B-A) = P(BᴒA´B) – P(A´ᴒB)
De 1 intercambiamo A y B:
P(B-A) = P(B) – P(AᴒB)
De 3 y 4:
P(A´ᴒB) = P(B) – P (AᴒB)
= 3/8-1/8 = 2/8 = ¼
b) De 2 P(A-B) = P (AᴒB´)
De 1 P(A-B) = P(A)-P (AᴒB)
Entonces:
P(AᴒB´) = P(A) – P (AᴒB)
= ¾-1/8 = 5/8 c) Sustituimos A por A´en 2:
P(A´-B) = P(A´ᴒB´)
Sustituimos A por A´ en 1:
P(A-´B) = P(A´) –P (A´ᴒB)
De (7) y (8) obtenemos:
P(A´ ᴒB´) = P(A´) – P (A´ ᴒ´B)
P(A´) = 1 – P(A) = 1 = -3/4 =1/4
d)(A´ᴗB) = P(A´) + P(B) –P (A´ᴒB)
Sustituyendo 10 y 5 en 12 tenemos:
P (A´ᴗB) = ¼+3/8-1/4=3/8 CONCLUSION
esta unidad se analizaron los conceptos básicos de probabilidad, y cómo se puede emplear el análisis de probabilidades para proporcionar ionformación útil para la toma de decisiones. • Se analizó la diferencia de la probabilidad aplicándose deque un suceso determinado ocurra y que simultáneamente otro suceso también determinado no ocurra.
Friday, September 30, 2011
Marco Antonio Díaz
- ESTATURASni15611571158216011652168116911701172117411801Totales13
Intervalo
|
mi
|
ni
|
fi
|
Ni
|
Fi
|
156
– 162
|
159
|
5
|
5/
13 = 0.384
|
5
|
5/
13 = 0.384
|
162
– 168
|
165
|
2
|
2/
13 = 0.153
|
7
|
7/
13 = 0.538
|
168
– 174
|
171
|
4
|
4/
13 = 0.307
|
11
|
11/13=0.846
|
174
– 180
|
177
|
1
|
1/
13 = 0.076
|
12
|
12/13=0.923
|
180
– 186
|
183
|
1
|
1/
13 = 0.076
|
13
|
13/13=1
|
Total
|
13
|
Escuela Nacional de Maestros
|
Escuela Normal Superior
|
Escuela Normal Privada
|
Especialización en la Universidad
Pedagógica Nacional
|
Hombre
|
Mujer
|
|
M1
|
X
|
X
|
X
|
|||
M2
|
X
|
X
|
X
|
X
|
||
M3
|
X
|
X
|
X
|
|||
M4
|
X
|
X
|
||||
M5
|
X
|
X
|
X
|
|||
M6
|
X
|
X
|
X
|
X
|
||
M7
|
X
|
X
|
X
|
|||
M8
|
X
|
X
|
||||
H1
|
X
|
X
|
X
|
X
|
||
H2
|
X
|
X
|
X
|
|||
H3
|
X
|
X
|
||||
H4
|
X
|
X
|
X
|
X
|
||
H5
|
X
|
X
|
||||
H6
|
X
|
X
|
X
|
|||
H7
|
X
|
X
|
X
|
X
|
||
H8
|
X
|
X
|
||||
H9
|
X
|
X
|
X
|
|||
H10
|
X
|
X
|
X
|
|||
18
|
12
|
6
|
6
|
12
|
10
|
8
|